Triángulo de vientos. Intro

Este nuevo post que escribo es para explicar el cálculo del triángulo de vientos (Wind Triangle) ya que a pesar de ser de suma utilidad, no he encontrado tanta información al respecto en bibliografía y por extraño que parezca, por Internet. Sí que podemos encontrar qué es y en qué se basa su cálculo pero a la hora de explicarlo, o se centran en un caso en particular o enseguida nos hablan de los flight computer tipo CR3 o E6B y se quedan tan panchos. Yo no voy a hacer eso, yo voy a explicar de manera matemática los cuatros casos de uso que nos podemos encontrar, bien en la realidad, bien en exámenes o ejercicios, y trataré de darle sentido a tanto ángulo, fórmula o teorema. O eso espero.

Dividiré los casos de uso en cuatro post distintos para poder diferenciar los distintas dudas o comentarios al respecto. Antes de empezar con el meollo de la cuestión es indispensable algo de teoría o más bien, definiciones de los conceptos más importantes.

En primer lugar el triángulo de vientos es un problema típico de cálculo en el que tratamos de averiguar un rumbo para seguir una ruta ya que nos encontramos bajo la influencia de un viento determinado. Los primeros conceptos que ya sacamos de esta definición son: rumbo y ruta. Puede que cueste un poco ver la diferencia pero en esencia, la ruta (Course) es la trayectoria deseada, es la proyección de la dirección de la aeronave sobre el suelo y marca una línea imaginaria entre los puntos origen y destino. Por otro lado rumbo (Heading) es la dirección seguida por el eje longitudinal de la aeronave, hacia donde apunta el morro y por tanto la dirección que seguiremos. En caso de que no exista viento o este sea prácticamente nulo, ruta y rumbo coinciden, pero esto es un supuesto ideal ya que raramente se cumple. Por muy leve que sea la intensidad del viento este crea una influencia en nuestra ruta provocando que nos alejemos de ella, cuanto más larga sea nuestra trayectoria a seguir mayor será la incidencia del viento.

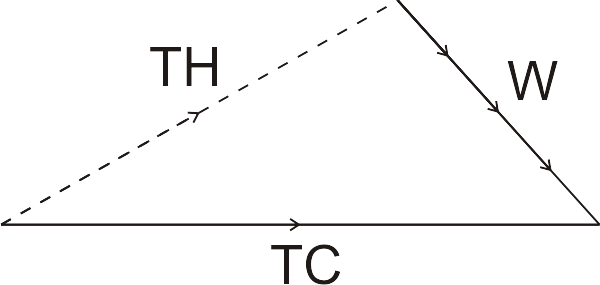
Cuando tratemos rumbos y rutas siempre haremos referencia a direcciones verdaderas (geográficas) y no magnéticas por tanto, la ruta verdadera la denotaremos como TC (True Course) y el rumbo verdadero como TH (True Heading). El viento (W, Wind)  será representado por un gradiente que indicará una dirección (Wd) y una intensidad (Ws) con el siguiente formato 090/15 representará un viento procedente del este (90º) y con una intensidad de 15 nudos. Veamos en la siguiente ilustración una representación típica del triángulo de vientos.

Al desplazamamiento que provoca el viento se le conoce como deriva (Drift) y es la diferencia angular entre rumbo y ruta. Para poder corregir este desplazamiento no deseado aplicaremos un movimiento corrector que llamaremos corrector de deriva (Drift Correction). Este será el ángulo que utilizaremos a lo largo de todos los cálculos. La manera de calcular este ángulo será TC – TH = dc.

Está claro que el avión no puede volar si no existe una fuerza que lo impulse, esta fuerza (empuje o tracción) genera la velocidad necesaria para que el viento relativo que rodea a la aeronave genere una fuerza de sustentación en la superficie alar. Para no entrar en principios de aerodinámica nos quedaremos simplemente con los conceptos de velocidad. En nuestro caso será importante saber que la velocidad que lleve una aeronave en el aire puede, y lo es, diferente a la que lleva respecto al suelo. La velocidad en el aire se denomina TAS (True Air Speed) y es una velocidad corregida para varios factores como error de instrumento, error de posición, compresibilidad y altitud de densidad, por otro lado tenemos la velocidad relativa al suelo o GS (Ground Speed) y no es más que la TAS a la que se le suma o resta la componente vertical del viento. Véase para ello mi post sobre componentes del viento 😉

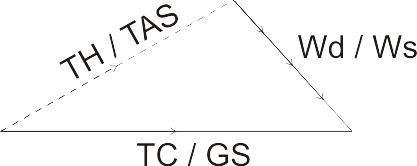
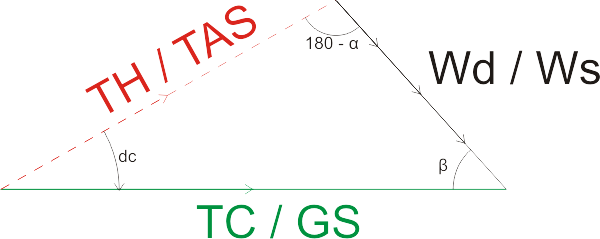
Todo esto de las velocidades es para darle sentido a la ilustración anterior ya que tenemos los ángulos de rumbo y ruta pero no el módulo de estos vectores de dirección, las magnitudes vienen dadas por la velocidad siendo TAS para el TH y GS para el TC. Así el triángulo de vientos quedaría de la siguiente forma:

Ya sabemos que el ángulo comprendido entre TH y TC es dc. Por otro lado el ángulo entre el TC y el W se llama β (Beta) y por último, el ángulo entre el TH y el W es α. Este ángulo en pocos sitios lo he visto explicado, pero es el ángulo que no pertenece al triángulo, el que está realmente «encerrado» en el triángulo será 180 – α. Creo que ahora sí que tenemos toda la información necesaria para visualizar un triángulo de vientos en condiciones.

Una vez aclarados los conceptos que componen el triángulo de vientos, ahora explicaré las herramientas que utilizaremos. El cálculo de este problema se puede hacer de tres maneras: usando un flight computer (CR3 o E6B), gráficamente utilizando papel milimetrado y matemáticamente. Esta es la opción que he elegido ya que es la menos divulgada y realmente la más precisa. De hecho esta manera es la más empleada hoy en día pero por los ordenadores de a bordo.

El método analítico consiste en aplicar las fórmulas y principios de trigonometría plana, en particular los teoremas del seno y coseno. El primero se basa en la relación de proporcionalidad entre las longitudes de los lados de un triángulo y los senos de los ángulos respectivamente opuestos. Y el segundo no es más que una generalización del teorema de Pitágoras. Veamos uno y otro teorema adaptados al caso que nos ocupa:

Teorema del seno:

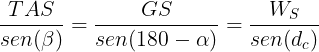
Teorema del coseno:

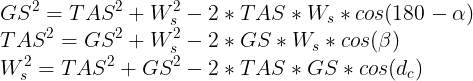
Otras fórmulas de interés son las que conciernen al cálculo de los ángulos:

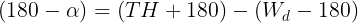
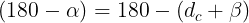
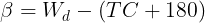
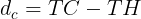
La metodología a emplear será la siguiente:

1. A partir de los datos conocidos se obtiene un ángulo de los tres que contiene el triángulo.
2. Ya con el ángulo anterior conoceremos como mínimo, dos lados y un ángulo.
3. En este momento se procede del siguiente modo:
   • Si se conocen dos lados y el ángulo comprendido entre ambos, aplicaremos el teorema del coseno para calcular el lado opuesto al ángulo conocido.
   • Si se conocen dos lados y un ángulo no comprendido entre ambos, aplicaremos el teorema del seno para calcular el otro ángulo.
4. Una vez hecho lo anterior se aplica el teorema contrario al empleado. O sea si empleamos el del coseno, continuaremos con el del seno y viceversa.

Bueno, creo que con esto podemos dar por finalizada esta introducción. Ahora a hacer ejercicios.